MARKET EFFICIENCY OF ASEAN STOCK MARKETS
1Research Scholar, Institute for Financial Management and Research, 25 , Kothari Road, Nungambakkam, Chennai, India , 2Senior Professor, Institute for Financial Management and Research, 24, Kothari Road, Nungambakkam, Chennai, India
ABSTRACT
In this paper, we examine the stock market efficiency of the members of the Association of South East Asian Nations (ASEAN). We use the conventional individual variance ratio tests like the Lo and MacKinlay (1988) test, Choi (1999) test, Wright (2000) test and Chen and Deo (2006)) test to check for the efficient market hypothesis in these markets. We also perform the spectral shape test of Durlauf (1991) and Average exponential test as in Andrews and Ploberger (1996) to check for the serial correlations in these stock indices. This study rejects the efficient market hypothesis for the stock markets of Indonesia, Malaysia, Philippines, Thailand and Vietnam. However, we find that the stock markets in Cambodia, Lao and Singapore are weak form efficient. This study is essential for the policy makers of ASEAN member nations who attempt to introduce new financial regulations to make their markets more attractive to the investors by making the stock markets efficient.
© 2017 AESS Publications. All Rights Reserved.
Keywords: Variance ratio tests, Random walk, Efficient market hypothesis, ASEAN, Spectral shape test, Average exponential test.
JEL Classification: C15, C58, G15.
Received: 9 September 2016/ Revised: 6 October 2016/ Accepted: 31 October 2016/ Published: 5 November 2016
Contribution/ Originality
This study contributes to the existing literature of the stock market efficiency of the member nations of the ASEAN region by employing individual variance ratio tests, spectral shape test and Average exponential test. This study documents that stock indices of Cambodia, Lao and Singapore are weak form efficient.
1. INTRODUCTION
Market efficiency has been an important area of research in the financial literature. It is only when the functioning of the markets is efficient, then no individual investor will have an upper hand over the other based on available information. According to the Efficient Market Hypothesis [EMH], any new information will immediately reflect in the price of the asset (Fama, 1970). Hence it becomes impossible to predict the price of an asset based on the past information. That is to say, the stock markets follow random walk in an efficient market.
In this paper, we examine the efficient market hypothesis for the Association of South East Asian Nations (ASEAN), which is the biggest regional community in the largest continent of the world with total nominal gross domestic product (GDP) of more than USD 2.8 trillion in 2015. According to Hill and Menon (2010) studies on financial integration and market development have been conducted by looking ASEAN nations as a group of economies. After the Asian financial crisis, in order to monitor the functioning of the financial sector activities, some of the ASEAN countries have introduced domestic regulatory frameworks. There was a huge surge in the number of listed companies, market capitalization and liquidity in the ASEAN member nations since then. Of the 10 ASEAN member nations, 8 nations have their own stock exchanges that include Cambodia, Indonesia, Lao, Malaysia, Philippines, Singapore, Thailand and Vietnam. Myanmar has started its own Yangon stock exchange in March 2016. Brunei has also announced of starting its own exchange but is not yet in function.
In order to achieve the goal of greater economic integration among the ASEAN member nations and the better development of sustainable capital markets, it is necessary to have efficiency in these ASEAN stock markets. It is known that if markets are inefficient, it becomes difficult to raise the capital through the markets which will hinder the viable investment projects. This paper also contributes to the existing literature in the area of market efficiency of the emerging stock markets and ASEAN member nations in particular. ASEAN is also chosen to bridge the gap in academic literature where majority of the work in efficient markets is done in the developed nations. The next section presents a brief review of literature. We then discuss the methodologies used in the study in Section 3. We discuss our data in Section 4 and provide empirical results in Section 5. Finally we conclude by providing some policy implications in the last section.
2. LITERATURE REVIEW
In this section we discuss some of the important contributions in the area of market efficiency present in the financial literature that focuses on the member nations of ASEAN community in particular. Though there exists many studies on emerging Asian markets, the results on the efficiency of these markets is mixed due to different methodologies that were employed in the literature and the difference in the study periods.
Huang (1995) have studied the random walk hypothesis for 8 Asian countries and Japan using Lo & MacKinlay variance ratio test for the period 1984-1998. Kawakatsu and Morey (1999) have performed Unit root test and multiple variance ratio tests on 16 emerging markets for the period 1976-1997. Malliaropulos and Priestley (1999) used Lo and MacKinlay (1988) test and Bootstrap methodology on Southeast Asian markets for the period 1988-1995. Worthington and Higgs (2004) have studied weak form market efficiency in Asian emerging and developed equity markets using serial correlation and unit root tests and concluded the emerging markets are not weak form efficient. A number of other studies on random walk hypothesis include the works of (Karemera and Ojah, 1999; Darrat and Zhong, 2000; Chang et al., 2004; Hoque et al., 2007).
Hamid et al. (2010) studied 14 Asian markets and concluded that monthly prices do not follow random walks. Nisar and Muhammed (2012) studied four South Asian markets and found that none of the markets follow random walk and hence are not weak form efficient for the period 1997-2011. Mishra (2012) performed analysis on five South Asian markets for the period 2005-2010 by using ADF, PP unit root tests and provide evidence that these markets are not weak form efficient. Paulo (2013) have used Unit root tests and Variance ratio tests for Asian stock markets and concluded that they are not weak form efficient. Amer (2014) studied 3 south Asian markets for period from 2003-2011 on monthly & weekly return indices and finds evidence that the markets are not weak form efficient. Kim and Shamsuddin (2008); Charles and Darnè (2009) have used the non-parametric (Wright, 2000) test in their analysis and found higher rate of rejection of random walk hypothesis. Overall the study on ASEAN nations in the literature is mixed due to the different methodologies and different time periods and data that were used in the study. In this paper, we employ multiple tests on daily data till date to get the efficiency of the individual ASEAN member nations
3. METHODOLOGY
In this section, we discuss the various methods that are used in this paper to examine the random walk hypothesis like Unit root test, Variance ratio test, Spectral shape test and Average exponential tests.
3.1. Augmented Dickey Fuller Unit Root test
The ADF unit root test Dickey and Fuller (1979) is carried out by estimating the below equation for which the null and alternate hypothesis is 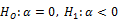 , where
, where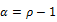 and evaluated using the conventional t-ratio for
and evaluated using the conventional t-ratio for 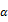 as
as 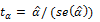 .
.
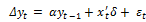
The presence of a unit root in a time series suggests support for the random walk hypothesis.
3.2. Variance Ratio Tests
The Variance ratio [VR] statistics and its advanced versions are widely used in the financial literature since the pioneer works of Lo and MacKinlay (1988;1989); Poterba and Summers (1988) and Cochrane (1988). The VR statistic in finance is used to test the market efficiency, i.e. to say whether the given time series of stock prices or its first difference (or returns) follow random walk.
Let 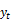 denote the logarithm of the stock price at time t. Let
denote the logarithm of the stock price at time t. Let 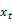 be an asset return at time t, where t=1, 2, ….., T, and defined as,
be an asset return at time t, where t=1, 2, ….., T, and defined as, 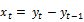 . The variance ratio (VR) can be expressed in terms of auto-correlation coefficients as explained in Lo and MacKinlay (1988) and defined as,
. The variance ratio (VR) can be expressed in terms of auto-correlation coefficients as explained in Lo and MacKinlay (1988) and defined as,
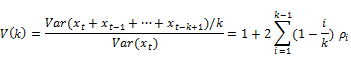
where 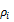 is the i-th lag auto-correlation coefficient of
is the i-th lag auto-correlation coefficient of 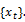 If the asset returns are uncorrelated over time then we have V(k) = 1.
If the asset returns are uncorrelated over time then we have V(k) = 1.
The variance ratio test statistic can further be constructed based on an estimator of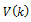 . Let
. Let 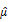 denote the sample mean of the asset returns defined as
denote the sample mean of the asset returns defined as 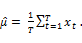 Let
Let 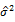 be the sample variance of the asset return. The sample variance of the one-period return can be defined as ,
be the sample variance of the asset return. The sample variance of the one-period return can be defined as ,
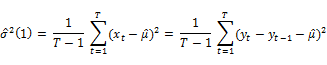
The sample variance of the k-period return can be defined as,
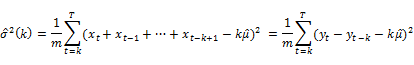
where we define the parameter 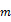 in such a way that
in such a way that 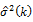 is an unbiased estimator of k-period return. i.e.
is an unbiased estimator of k-period return. i.e.
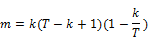
The central idea of testing the random walk hypothesis using the variance ratio [VR] statistic against the stationary alternatives lies in utilizing the fact that the variance of the random walk increments is linear in all sampling intervals. That is to say, the sample variance of k-period return is k-times the sample variance of the one-period return. The variance ratio at lag k, i.e. VR (k) is then defined as the ratio of (1/k) times the sample variance of the k-period return to the sample variance of the one-period return.
The variance ratio is defined as
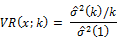
Hence the VR will be equal to 1 for all values of k, when the asset returns follow the random walk. If the VR is less than 1, then we have indications of negative serial correlation (mean-reversion). If the VR is more than 1, then we have indications of the positive serial correlation (mean-aversion).
The VR statistic as explained in Wright (2000) can be defined as
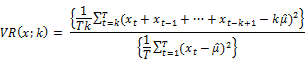
Let us describe the individual VR tests developed by Lo and MacKinlay (1988) as well as some of its advancements.
3.2.1. Lo and MacKinlay (1988) Variance Ratio Test
Lo & MacKinlay proposed the asymptotic distribution of 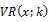 by assuming that k is fixed when
by assuming that k is fixed when  They showed that if
They showed that if 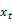
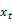 is i.i.d., i.e. under the assumption of homoscedasticity, then under the null hypothesis that
is i.i.d., i.e. under the assumption of homoscedasticity, then under the null hypothesis that 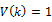 , the test statistic
, the test statistic 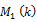 is given by
is given by
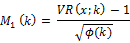
which follows the standard normal distribution asymptotically. The asymptotic variance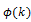 , is given by
, is given by
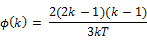
Lo and MacKinlay (1988) proposed the heteroscedasticity robust test statistic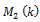 , to accommodate
, to accommodate 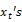 exhibiting the conditional heteroscedasticity as,
exhibiting the conditional heteroscedasticity as,
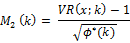
which follows the standard normal distribution asymptotically under null hypothesis that 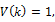 where
where
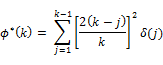
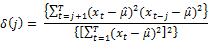
3.2.2. Choi (1999) Test
The choice of holding period k when implementing the VR tests is important but is rather chosen arbitrarily. Hence to overcome this issue, Choi (1999) proposed a data dependent procedure to determine the optimal value of k.
The VR estimator is defined as
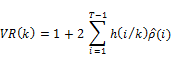
Where 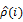 is the auto-correlation function, and
is the auto-correlation function, and 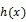 is the Quadratic Spectral kernel defined as
is the Quadratic Spectral kernel defined as
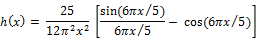
The standardized statistic is
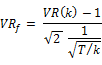
Under the null hypothesis the test statistic 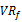 follows the standard normal distribution asymptotically. Note that it is assumed that as
follows the standard normal distribution asymptotically. Note that it is assumed that as 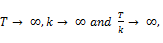 the small sample properties of this automatic VR test under heteroscedasticity are unknown and not investigated properly.
the small sample properties of this automatic VR test under heteroscedasticity are unknown and not investigated properly.
3.2.3. Wright (2000) Test
Wright (2000) proposed a non-parametric alternative to conventional asymptotic VR tests using signs and ranks. The tests based on ranks are exact under the i.i.d. assumption, whereas the tests based on signs are exact under conditional hetereoscedasticity. Wright (2000) proposed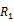 and
and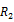 statistics defined as
statistics defined as
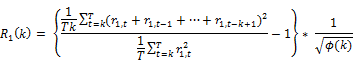
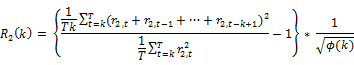
Where the standardized ranks are given by
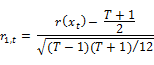
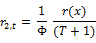
Where
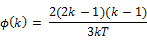
And 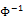 is the inverse of the standard normal cumulative distribution function.
is the inverse of the standard normal cumulative distribution function.
The tests based on signs of the first difference is given by
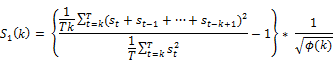
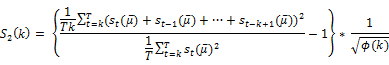
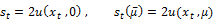
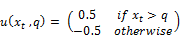
Note that the critical values of 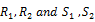 can be obtained by simulating its exact sampling distributions.
can be obtained by simulating its exact sampling distributions.
3.2.4. Chen and Deo (2006) Test
It is very important to note that the conventional VR tests such as the Lo & MacKinlay test are asymptotic tests in that their sampling distributions are approximated by their limiting distributions. Indeed, the practical use of the statistic has been impeded by the fact that the asymptotic theory provides a poor approximation to the small-sample distribution of the VR statistic. In general, the ability of the asymptotic distribution to approximate the finite sample distribution depends crucially on the value of the horizon k. More specifically, rather than being normally distributed (when standardized by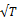 ) as the theory states, the statistics are severely biased and right skewed for large k (relative to T) (Lo and MacKinlay, 1989) which makes application of the statistic problematic. In other words, the finite-sample null distribution of the test statistic is quite asymmetric and non-normal.
) as the theory states, the statistics are severely biased and right skewed for large k (relative to T) (Lo and MacKinlay, 1989) which makes application of the statistic problematic. In other words, the finite-sample null distribution of the test statistic is quite asymmetric and non-normal.
Chen and Deo (2006) suggested a simple power transformation of the VR statistic that, when k is not too large, provides a better approximation to the normal distribution in finite samples and is able to solve the well-known right skewness problem. They showed that the transformed VR statistic leads to significant gains in power against mean reverting alternatives. Furthermore, the distribution of the transformed VR statistic is shown, both theoretically and through simulations, to be robust to conditional heteroscedasticity.
First, they defined the VR statistic based on the periodogram as
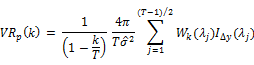
To obtain the transformed VR statistic, the following power transformation to 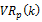 is applied,
is applied,
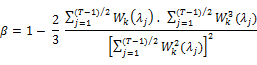
3.3. Spectral Shape Tests
The spectral shape tests as introduced in Durlauf (1991) are designed to test the serial correlation. These tests are completely data dependent and there is no parameter that researcher needs to select. The tests we use are
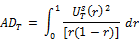
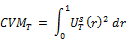
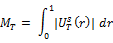
Where
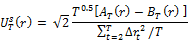
We have
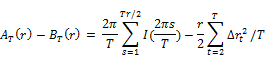
And
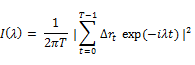
The 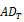 and
and 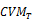 tests are studied in Durlauf (1991) and the
tests are studied in Durlauf (1991) and the 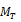 test in Choi and Mark (1997).
test in Choi and Mark (1997).
3.4. Average Exponential Tests
These tests essentially combine either the likelihood ratio (LR) tests or the Lagrange multiplier (LM) such that an optimality property is achieved. Though the Andrews and Ploberger (1996) tests are devised for the ARMA(1,1) alternative under a normality assumption, they are consistent against all weakly stationary and strong mixing alternatives. Among the tests introduced in Andrews and Ploberger (1996) we will employ the average exponential likelihood ratio and Lagrange multiplier. The average exponential LR and LM tests are
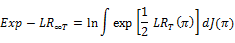
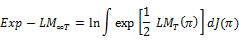
Where
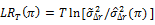
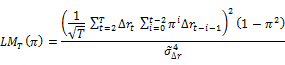
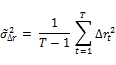
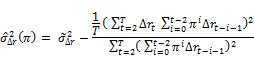
And 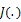 is the uniform measure on
is the uniform measure on 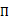 which is the parameter space on π.
which is the parameter space on π.
4. DATA DESCRIPTION
In this section, we describe the data that we have used for our empirical analysis. We have collected the daily closing prices data of 8 ASEAN stock indices for the period mentioned in the brackets; namely Cambodia’s CSX Index (2012-2016), Indonesia’s JCI Index (1990-2016), Lao’s LSXC Index (2011-2016), Malaysia’s FBMKLCI Index (1994-2016) , Philippines’s PCOMP Index (1990-2016), Singapore’s STI Index (1999-2016), Thailand’s SET50 Index (1995-2016) and Vietnam’s VNIN Index (2000-2016). The daily data is collected from the source Bloomberg. In Table 1: we provide the descriptive statistics of the 8 ASEAN stock indices under consideration. We observe negative skewness in Cambodia, Indonesia, Singapore and Vietnam. The kurtosis was higher in Malaysia, Indonesia, Philippines and Thailand. We observe that all the stock indices are non-normal as per the results of Jarque-Bera test.
5. EMPIRICAL FINDINGS
In this section, we present the empirical results as per the tests mentioned in the methodological section. In Table 2, we show the results of the Augmented Dickey Fuller Unit root test. We observe that for the three models i.e. {None, Drift, Trend}, the test statistic are significant at 1% level of significance for all the 8 member nations of ASEAN. Hence we reject the null hypothesis of unit root in all 8 nations to support the altenative of stationarity. The ADF test results indicate that the ASEAN stock market returns donot follow the random walk process.
Table-1. Descriptive Statistics
| Cambodia | Indonesia | Lao | Malaysia | Philippines | Singapore | Thailand | Vietnam | |
| No of Obs | 974 | 6487 | 1390 | 5579 | 6583 | 4262 | 5144 | 3820 |
| Mean | -0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Maximum | 0.049 | 0.131 | 0.063 | 0.208 | 0.162 | 0.075 | 0.126 | 0.067 |
| Minimum | -0.051 | -0.127 | -0.063 | -0.242 | -0.131 | -0.087 | -0.172 | -0.077 |
| Std Dev | 0.015 | 0.015 | 0.013 | 0.013 | 0.015 | 0.012 | 0.018 | 0.016 |
| Skewness | -0.313 | -0.071 | 0.210 | 0.461 | 0.157 | -0.254 | 0.209 | -0.257 |
| Kurtosis | 2.645 | 9.242 | 3.825 | 53.227 | 8.788 | 5.017 | 7.252 | 2.660 |
| Jarque Bera | 302.261 | 23112.330 | 861.854 | 659272.700 | 21228.290 | 4521.778 | 11323.350 | 1170.563 |
| p-value | 0.000*** | 0.000*** | 0.000*** | 0.000*** | 0.000*** | 0.000*** | 0.000*** | 0.000*** |
*** represents 1% level of significance. Stock returns are calculated using the formula
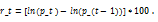
Source: Developed by the authors
Table-2. Augmented Dickey Fuller Unit Root test
| Model | Cambodia | Indonesia | Lao | Malaysia | Philippines | Singapore | Thailand | Vietnam |
| None | -19.69* | -51.83* | -24.93* | -50.05* | -53.70* | -45.08* | -47.03* | -38.19* |
| Drift | -19.85* | -51.87* | -24.92* | -50.04* | -53.72* | -45.07* | -47.03* | -38.22* |
| Trend | -19.91* | -51.88* | -24.94* | -50.06* | -53.73* | -45.07* | -47.07* | -38.24* |
Critical values for the model-"None" are -2.58 (1%) and -1.95 (5%). Critical values for the model-"Drift" are
-3.43(1%) and -2.86(5%). Critical Values for the model-"Trend" are -3.96 (1%) and -3.41 (5%). * represents significance at 1% level of significance. Augmented Dickey Fuller (ADF) test is performed on the stock returns.
Source: Developed by the authors.
In Table 3, we present the details of Lo & Mackinlay variance ratio test results for k-day =2, 4, 6, 8 and 10. We test the null hypothesis that variance ratio is equal to 1.If we consider the M1 statistic which is based on the homoscedastic assumption, random walk hypothesis is rejected for Indonesia, Malaysia, Philippines, Thailand and Vietnam for all the k-day windows as we find the test statistic to be significant.Also for Cambodia , M1 statistic is significant for k-day =4 and 6 ; for Lao, it is significant for k-day=6,8 & 10 and for Singapore, it is significant for k-day =6 ,8. That is to say, we get mixed results for diffferent k-days for Cambodia, Lao and Singapore when we consider the homoscedastic assumption. We also present the results of M2 statistic, which is based on the heterosedastic assumption. The M2 statistic is found to be significant in Indonesia, Philippines, Thailand and Vietnam and hence we reject the random walk hypothesis. Overall, we can conclude that the random walk hypothesis is rejected in all ASEAN nations except for Cambodia, Lao and Singapore. In case of Malaysia we have mixed results as M1 rejects the random walk hypothesis where as M2 statistic doesnot based on Lo & Mackinaly variance ratio test.
In Table 4, we show the results of the individual variance ratio tests namely (Choi, 1999) Automatic Variance ratio test and Chen and Deo (2006) power transformed joint variance ratio test. We observe that the random walk hypothesis is rejected in all ASEAN stock markets based on Automatic variance ratio test as the test statistics are significant at 1% level of significance, except for Cambodia, Lao and Singapore. In case of the Chen and Deo (2006) test, we observe that random walk hypothesis is rejected for Indonesia, Philippines and Vietnam at 1% level of significance and Thailand at 5% level of significance. However, we find weak form market efficiency in Cambodia, Lao, Malaysia and Singapore.
Table-3. Lo & MacKinlay Variance Ratio
| No of holding period days i.e. k-days | ||||||||
| k=2 | k=4 | k=6 | k=8 | k=10 | ||||
| Cambodia | ||||||||
| VR(k) M1 M2 |
1.009 0.285 0.183 |
1.121 2.024** 1.290 |
1.161 2.036** 1.306 |
1.170 1.791 1.160 |
1.114 1.056 0.693 |
|||
| Indonesia | ||||||||
| VR(k) M1 M2 |
1.165 13.253** 7.444** |
1.267 11.499** 6.486** |
1.279 9.087** 5.186** |
1.267 7.280** 4.215** |
1.266 6.354** 3.726** |
|||
| Lao | ||||||||
| VR(q) M1 M2 |
1.025 0.925 0.472 |
1.094 1.879 0.987 |
1.144 2.171** 1.171 |
1.177 2.231** 1.225 |
1.184 2.036** 1.133 |
|||
| Malaysia | ||||||||
| VR(k) M1 M2 |
1.173 5.423** 1.021 |
1.251 5.383** 1.100 |
1.278 3.677** 0.801 |
1.281 2.608** 0.597 |
1.303 2.043** 0.490 |
|||
| Philippines | ||||||||
| VR(k) M1 M2 |
1.173 14.024** 9.312** |
1.251 10.883** 7.163** |
1.278 9.131** 6.058** |
1.281 7.697** 5.186** |
1.303 7.283** 4.979** |
|||
| Singapore | ||||||||
| VR(k) M1 M2 |
1.028 1.811 1.149 |
1.052 1.811 1.099 |
1.085 2.257** 1.354 |
1.091 2.009** 1.206 |
1.097 1.882 1.135 |
|||
| Thailand | ||||||||
| VR(k) M1 M2 |
1.084 6.038** 3.071** |
1.159 6.116** 3.267** |
1.171 4.973** 2.770** |
1.159 3.850** 2.220** |
1.162 3.459** 2.048** |
|||
| Vietnam | ||||||||
| VR(k) M1 M2 |
1.294 18.180** 9.428** |
1.499 16.481** 8.750** |
1.666 16.656** 8.987** |
1.830 17.343** 9.454** |
1.955 17.488** 9.622** |
|||
** represents 5% level of significance. VR (k) is the Lo & Mackinlay variance ratio statistic. M1 is the test statistic for homoscedasticity assumption whereas M2 is the test statistic for heteroscedasticity assumption.
Table-4. The results of Choi (1999) test and Chen and Deo (2006) variance ratio test:
| Choi (1999) Test | Chen and Deo (2006) | |||||
| Automatic Variance Ratio Test | Power Transformed Joint Variance Ratio test | |||||
| stat | sum | Vrsum | Qpn | |||
| Cambodia | 0.140 | 1.008 | 0.135 | 4.584 | ||
| Indonesia | 7.603** | 1.318 | 0.228 | 52.531** | ||
| Lao | 0.641 | 1.032 | 0.170 | 6.017 | ||
| Malaysia | 4.351** | 1.157 | 0.105 | 1.864 | ||
| Philippines | 7.440** | 1.314 | 0.231 | 84.358** | ||
| Singapore | 1.295 | 1.042 | 0.067 | 3.821 | ||
| Thailand | 5.224** | 1.202 | 0.137 | 14.188* | ||
| Vietnam | 15.620** | 1.970 | 0.501 | 86.871** | ||
**, * represents 1%, 5% level of significance respectively. 'stat' represents the Automatic variance ratio test statistic. 'sum' is the 1+ weighted sum of autocorrelation up to the optimal order. 'Vrsum' is the sum of power transformed individual VR-1.
Source: Developed by authors
In Table 5, we present the results of Spectral shape tests as proposed in Durlauf (1991). We observe that the random walk hypothesis is rejected in all ASEAN nations except for Cambodia, Lao and Singapore. We find that Mellows M statistic is significant for Indonesia (3.663) and Philippines (3.980) at 1% level of significance whereas for Malaysia and Thailand, M statistic is significant at 5% level of significance. We also show the results of Average exponential test as proposed in Andrews and Ploberger (1996). It clearly shows that there exists weak form efficiency only in Cambodia, Lao and Singapore as the test statistic in other ASEAN nations are significant.
Table-5. The results of Spectral shape test and Average Exponential test
| Durlauf (1991) | Andrews and Ploberger (1996) | ||||||
| Spectral Shape Test | Average Exponential Test | ||||||
| AD | CVM | M | Ex.LM | Ex.LR | |||
| Cambodia | 2.519 | 0.348 | 0.507 | 1.622 | 1.390 | ||
| Indonesia | 82.221** | 17.325** | 3.663** | 88.801** | 87.574** | ||
| Lao | 3.393 | 0.342 | 0.388 | 4.708 | 3.455 | ||
| Malaysia | 18.258** | 3.422** | 1.618* | 14.465** | 15.822** | ||
| Philippines | 96.592** | 20.472** | 3.980** | 96.485** | 100.243** | ||
| Singapore | 2.064 | 0.377 | 0.549 | 1.653 | 1.605 | ||
| Thailand | 19.345** | <4.018** | 1.750* | 19.081** | 18.279** | ||
| Vietnam | 176.257** | 34.245** | 5.326** | 178.645** | 174.391** | ||
**, * represents 1%, 5 % level of significance respectively. AD is the Anderson-Darling statistic. CVM is the Cramer-von Mises statistic. M is the Mellows statistic. LM is the Lagrange Multiplier test. LR is the likelihood ratio test.
Source: Developed by authors
In Table 6, we show the results of Wright (2000) Rank and Sign test. Based on the results of rank tests R1 and R2, we can observe that the random walk hypothesis is rejected in Indonesia, Malaysia, Philippines, Thailand and Vietnam. We can find that there exists weak form efficiency in Cambodia, Lao and Singapore. However when we look at the results of sign test S1, we reject the random walk hypothesis in all ASEAN nations including Cambodia and Lao except at Singapore. So overall, we find Singapore as the weak form efficient market based on Wright (2000) Rank and Sign test.
6. CONCLUSION
This paper examines the market efficiency in the ASEAN-8 nations that include Cambodia, Indonesia, Lao, Malaysia, Philippines, Singapore, Thailand and Vietnam. The ADF unit root test rejects the random walk hypothesis in all the ASEAN markets under study. We have used the individual variance ratio tests which are considered to be more powerful than the unit root tests. We observe that Lo and MacKinlay (1988) variance ratio test and Choi (1999) Automatic variance ratio test give similar results in which out of the 8 ASEAN nations only 3 nations (i.e. Cambodia, Lao and Singapore) stock markets are found to be weak form efficient. Durlauf (1991) spectral shape test, Andrews and Ploberger (1996) Average exponential test also confirms that the 3 ASEAN nations are weak form efficient like the results of Choi (1999) test. In Wright (2000) rank and sign based test, we have found that all the ASEAN nations are inefficient, except Singapore.
In Chen and Deo (2006) power transformed joint variance ratio test, Malaysian stock market is also found to be efficient apart from Cambodia, Lao and Singapore stock markets. Overall based on various market efficiency tests employed in this study, we can conclude that stock markets in Cambodia, Lao and Singapore are consistently found to be weak form efficient. We have found mixed results in case of Malaysian stock market with regards to its efficiency based on multiple random walk tests. The rest of the ASEAN stock markets namely; Indonesia, Philippines, Thailand and Vietnam are found to be inefficient.
With the continuous increase of the foreign direct investment (FDI) in ASEAN region, it becomes essential to safeguard the wealth of the investors. The policy makers should introduce legal and regulatory frameworks which can bring positive sentiment for potential investors. Hence it is very important to make the stock markets in this ASEAN economic block efficient.
Table-6. The results of Wright (2000) Rank and Sign test:
|
||||||||||||||||||||||||||||||
| ** represents 5% level of significance. R1, R2 and S1 are rank and sign statistics of Wright (2000) test.Source: Developed by authors |
| Funding: This study received no specific financial support. |
| Competing Interests: The authors declare that they have no competing interests. |
| Contributors/Acknowledgement: All authors contributed equally to the conception and design of the study. |
REFERENCES
Amer, S., 2014. Efficiency of South Asian capital markets: An empirical analysis. European Journal of Business and Management, 6(11): 30-33.
Andrews, D.W.K. and W. Ploberger, 1996. Testing for correlation against an arma (1,1) process. Journal of the American Statistical Association, 91(435): 1331-1342.
Chang, E.J., E.J. Arauio-Lima and B.M. Tabak, 2004. Testing for predictability in emerging equity markets. Emerging Market Review, 5(3): 295-316.
Charles, A. and O. Darnè, 2009. The random walk hypothesis for Chinese stock markets: Evidence from variance ratio tests. Economic Systems, 33(2): 117-126.
Chen, W.W. and R.S. Deo, 2006. The variance ratio statistic at large horizons. Econometric Theory, 22(2): 206-234.
Choi, I., 1999. Testing the random walk hypothesis for real exchange rates. Journal of Applied Econometrics, 14: 293-308.
Choi, I. and N. Mark, 1997. Frequency domain tests for residual serial correlation in cointegration regressions. Oxford Bulletin of Economics and Statistics, 59(4): 549-562.
Cochrane, J.H., 1988. How big is the random walk in GNP? Journal of Political Economy, 96(5): 893-920.
Darrat, A.F. and M. Zhong, 2000. On testing the random walk hypothesis: A model comparison approach. Financial Review, 35(3): 105-124.
Dickey, D. and W.A. Fuller, 1979. Distribution of the estimates for autoregressive time series with a unit root. Journal of the American Statistical Association, 74(366): 427-431.
Durlauf, S., 1991. Spectral based testing of the martingale hypothesis. Journal of Econometrics, 50(3): 355-376.
Fama, E.F., 1970. Efficient capital markets: A review of theory and empirical work. Journal of Finance, 25(2): 383–417.
Hamid, K., M.T. Suleman, S.S.Z. Ali and R.S. Akash, 2010. Testing the weak form of efficient market hypothesis: Empirical evidence from Asia-pacific markets. International Research Journal of Finance and Economics: 121-133.
Hill, H. and J. Menon, 2010. ASEAN economic integration: Features, fulfillments, failures and future. ADB Working Paper Series on Regional Economic Integration, 69: 1-44.
Hoque, H., H.K. Jae and C.S. Pyun, 2007. A comparison of variance ratio tests of random walk: A case of Asian emerging stock markets. International Review of Economics and Finance, 16(4): 488-502.
Huang, B.N., 1995. Do Asian stock market prices follow random walks? Evidence from variance ratio test. Applied Financial Economics, 5(4): 251–256.
Karemera, D. and K. Ojah, 1999. Random walks and market efficiency tests: Evidence from emerging equity markets. Review of Quantitative Finance and Accounting 13(2): 171-188.
Kawakatsu, H. and M.R. Morey, 1999. An empirical examination of financial liberalization and efficiency of emerging market stock prices. Journal of Financial Research, 22(4): 358–411.
Kim, H.J. and A. Shamsuddin, 2008. Are Asian stock markets efficient? Evidence from new multiple varaince ratio tests. Journal of Empirical Finance, 15(3): 518-532.
Lo, A.W. and C.A. MacKinlay, 1988. Stock market prices do not follow random walk: Evidence from a simple specification test. Review of Financial Studies, 1(1): 41-66.
Lo, A.W. and C.A. MacKinlay, 1988;1989. Stock market prices do not follow random walk: Evidence from a simple specification test. Review of Financial Studies, 1: 41-66.
Lo, A.W. and C.A. MacKinlay, 1989. The size and power of the variance ratio test in finite samples: A Monte Carlo investigation. Journal of Econometrics, 20(2): 203-238.
Malliaropulos, D. and R. Priestley, 1999. Mean reversion in Southeast Asian stock markets. Journal of Empirical Finance, 6(4): 355–384.
Mishra, P.K., 2012. Efficiency of South Asian capital markets. Pakistan Journal of Commerce and Social Sciences, 6(1): 27-34.
Nisar, S. and H. Muhammed, 2012. Testing weak form of efficient market hypothesis: Empirical evidence from South-Asia. World Applied Sciences Journal, 17(4): 414-427.
Paulo, V., 2013. The efficiency of Asian stock markets: A weak-form efficiency analysis. IJER, 10(1): 117-136.
Poterba, J.M. and L.H. Summers, 1988. Mean reversion in stock prices: Evidence and implications. Journal of Financial Economics, 22(1): 27-59.
Worthington, A. and H. Higgs, 2004. Random walks and market efficiency in European equity markets. Global Journal of Finance and Economics, 1(1): 59-78.
Wright, J.H., 2000. Alternative variance-ratio tests using ranks and signs. Journal of Business & Economics Statistics, 1(1): 1-9.
| Views and opinions expressed in this article are the views and opinions of the author(s), Asian Economic and Financial Review shall not be responsible or answerable for any loss, damage or liability etc. caused in relation to/arising out of the use of the content. |






