DYNAMICS OF THE RELATIONSHIP BETWEEN IMPLIED VOLATILITY INDICES AND STOCK PRICES INDICES: THE CASE OF EUROPEAN STOCK MARKETS
1Assistant professor, Institut supérieur de finance et fiscalité Sousse, Tunisia , 2PHD student, Institut des Hautes Etudes Commerciales de Carthage, Tunisia
ABSTRACT
This paper examines the relationship between implied volatility indices and stock price indices in the case of five European market : Euro zone, France, Germany, Switzerland and the United Kingdom for the period from January 2010 to March 2015. To achieve that, two empirical models were estimated. Using GARCH modelling, our results show clearly that implied volatility indices contain relevant information concerning future stock market volatility, while this information is still insufficient in predicting the latter. A multiple linear regression procedure confirmed the existence of a strong negative and asymmetrical relationship between the implied volatility indices and stock market returns for three studied markets.
© 2017 AESS Publications. All Rights Reserved.
Keywords: Implied volatility indices, Stock market returns, Volatility asymmetry, Volatility feedback, European equity markets.
JEL Classification: G2, G13, G17.
Received: 26 May 2016/ Revised: 2 July 2016/ Accepted: 22 September 2016/ Published: 5 November 2016
Contribution/ Originality
This study contributes to the existing literature in two ways: we propose the first paper focusing on the relationship between implied volatility indices and stock indices in the case European markets. Secondly, the study is not about a single market, but rather five among the largest in the Euro zone.
1. INTRODUCTION
In a context of increased uncertainty, traders become more attentive to asset prices volatility which is considered as crucial information affecting asset allocation, hedging and portfolios diversification. Therefore, an adequate estimate of the volatility contributes to more efficient financial strategies.
We propose to study the ability of volatility indices to predict financial assets volatility. However, measures used in the literature could be classified into two categories: the first is based on historical volatility, while the second on derivatives implied volatility. Indeed, the first was assimilated to returns’ standard deviation (Hull (2011)) the latter considers the volatility of the underlying asset as reflected by option prices (Aboura (2005)).
Importance of implied volatility has been underlined through the development of new financial instruments namely implied volatility indices. This allows option traders to follow the market trend performing underlying stock price expectations.
These newly created volatility indices were implemented by the "Chicago Board Options Exchange" (CBOE) in 2003, in order to calculate the US implied volatility index VIX on the bases of the approach of "Model-Free Implied Volatility" (MFIV). Such developments in the financial industry have prompted a new area of research aiming to identify the relationship between volatility indices and the corresponding stock markets ones. In particular, implied volatility indices are often considered to be forward-looking measures of the expected market volatility (see Whaley (1993); Simon (2003); Giot (2005) etc..).
In addition, they are also named indices of investors’ fear (Whaley (2000)) to the extent that they reflect the sentiments of investors managing the stock market variations Baker and Wurgler (2006). Thus, these features give them the privilege of being used as barometers of representative stock markets. Recent studies have attempted to explain the performance of volatility indices in forecasting future stock market volatility. They have been often compared to other estimates of the volatility measures namely historical volatility and ARCH / GARCH models. Another research component was also discussed in the recent financial literature dealing with the relationship between implied volatility indices and stock market returns. The main idea was that the first are likely to contain relevant information about the stock market ("Spot"). Thus, information provided by the latter remains important in attracting the attention of various categories of stakeholders (hedgers, speculators, arbitrageurs). However, most empirical studies investigating this research axis focused especially on the US market and other emerging markets (India, Korea and Japan), while studies on stock markets Europeans remain poorly treated.
It is in this framework we will explore the importance of implied volatility indices in explaining stock market returns on the one hand, and underlying stocks’ volatility on the other hand. Empirical validation is conducted in the case of five stock markets from the euro area namely: Euro zone, France, Germany, Switzerland and the United Kingdom during the period extending from 1 January 2010 to 31 March 2015. The main objective of this paper is to check whether implied volatility indices help explaining future volatility and stock returns. It is organized as follows: section 1 provides a short review of the literature, Section 2 describes the data and the methodology used and the last section concludes the paper.
2. LITERATURE REVIEW
A new direction of financial literature stems from the fact that the implied volatility indices are considered both as forward-looking measures of the volatility of the overall market as well as an indicator of investor sentiment. This has revived the interest of several academic studies to explore the informational role of implicit volatility indices in terms of explaining future volatility and stock market returns. In the same context we propose to revisit results of some empirical studies.
First, several theoretical and academic studies have examined the performance of implied volatility indices in forecasting future stock market volatility although empirical findings on this issue are still controversial. For their part, Corrado and Miller (2005) examined three US implied volatility indices namely VXN, VIX and VXO between January 1988 and December 2003. They found that the three implied volatility indices are efficient estimators of the stock market future volatility considering a GARCH modelling. In other words, these volatility indices contain relevant information but don’t reflect all information set on the volatility of the US stock market. They also found that the VXN index provides significantly more efficient forecasting realized volatility compared to VIX and VXO indices. Another study in the context of the Korean market by Maghrebi et al. (2007) during the period from July 7, 1997 to June 30, 2006 suggests that the index KOSPI 200 New IV contains relevant information about future volatility which is not reflected by the volatility generated by different specifications of the GARCH model. Similarly, Siriopoulos and Fassas (2008) studied the predictive power of implied volatility index VFTSE, observed on the UK stock market, with regard to future volatility between February 2000 and May 2008. In addition, they found that this volatility index is a biased but efficient estimator of realized volatility. Similarly, it contains all the information regarding the future volatility that is not included in the historical volatility. More recently, Frijns et al. (2010) examined the performance of the information content of the implied volatility index AVX calculated from options market prices from the Australian stock index S & P / ASX 200, compared to alternative models for volatility forecasting (the GARCH models and "RiskMetrics" approach) for various forecast horizons. Thus, in sample empirical results showed that implied volatility index contains additional information with respect to the model GJR-GARCH (1,1). Furthermore, through the out of sample ones Frijns et al. (2010) noted that implied volatility index AVX is the best predictor of future realized volatility dominating volatility forecasting under the approach "RiskMetrics" and GJR-GARCH (1,1).
Thus, Banerjee and Kumar (2011) compared the performance of GARCH conditional volatility model (1.1) and the Indian implied volatility index VIX forecasting future volatility of the Nifty 50 representative of the stock market India. They found that VIX index represents a good estimator of future volatility generated by the GARCH (1,1). Similarly, the study of Ryu (2012) conducted in the case of the Korean stock market over the period of January 3, 2003 to April 12, 2011 showed that the relative index VKOSPI provides forecasts of future realized volatility slightly biased by dominating those generated by the implied volatility of the Black and Scholes (1973) "RiskMetrics" approach, and GJR-GARCH (1,1). Another recent study by Thenmozhi and Chandra (2015) compared performance of the information content of the Indian one (India VIX) compared to traditional measures of volatility. They found that the first is more efficient in terms of forecasting future market volatility compared to other conditional volatility derived from GARCH and EGARCH models.
However, several empirical studies have shown that implied volatility indices are less informative with regard to future stock market volatility compared to other alternative ones. In the same vein, a study conducted in the US market by Dowling and Muthuswamy (2005) calculated implied volatility index AVIX using the same methodology that VIX-New. They found that the AVIX index represents a poor estimator of future volatility relative to those from autoregressive models. In addition, Koopman et al. (2005) on the basis of a study conducted in the US market during the period from January 6, 1997 to November 15, 2003, they found that implied volatility index VIX contains additional information in relation to a stochastic volatility model. However, this result is not confirmed using GARCH specification. Therefore volatility index is not the best measure for forecasting future volatility of the US stock market. Similarly, Becker et al. (2007) through a study conducted during the period from 2 January 1990 to 17 October 2003 found that implied volatility index VIX doesn’t contain any additional information compared to different volatility forecasting models. This result indicates that option market (on the S&P 500) is unable to anticipate the movements of the stock market future volatility. Therefore, they considered these markets as inefficient. More recently, the study of Padhi and Shaikh (2014) using a time period from 4 June 2001 to 31 May 2011, showed that implied volatility of call and put options on the currency from S & P CNX Nifty contains relevant information about future realized volatility based on underlying stock index returns. In contrast, the historical volatility contains additional information with respect to the latter. Referring to the first part of the literature review, we propose to validate the following assumptions:
H1: The implied volatility index contains additional information compared to the volatility generated by the GARCH models.
H2: The implied volatility index is the best measure of forecasting future stock market volatility.
On this research area, a variety of empirical works has addressed the relationship between implied volatility indices and returns of the corresponding stock market. Simon (2003) suggested that daily variations of VXN implied volatility index respond asymmetrically to positive and negative returns variations of the Nasdaq 100 Index both during and after the bursting of the Internet bubble respectively. Similarly, Giot (2005) also showed that there is a strong negative relationship between contemporary variations of two implied volatility indices VIX, VXN and returns of the underlying stocks indices S & P 100 and Nasdaq 100. Indeed, it showed that this asymmetric relationship intuitively depends on the considered period: it is much more important for a bull market than a bear one. In the same vein, Dowling and Muthuswamy (2005) and considering the Australian market, they showed that the volatility index AVIX variations induce a negative impact on returns of the S & P / ASX 200. No evidence of an asymmetric effect was found in this case. Also, Hibbert et al. (2008) underlined, using several econometric approaches, a negative and asymmetrical relationship between the implied volatility index VIX-New and VXN-New and returns of the underlying stock indices S & P 500 and Nasdaq 100. However, they showed that assumptions of leverage and volatility feedback are unable to explain the relationship between implied volatility indices of contemporary returns and corresponding underlying assets indices. Moreover, for the German stock market, Masset and Wallmeier (2010) examined the possible causal links between variations in the index of implied volatility calculated from the price of opting on the DAX 30 and the contemporaneous returns index DAX 30 between 1995 and 2005. Using a VAR specification they concluded that returns from DAX 30 calculated over 5 minutes intervals granger causes the implied volatility index variation. The assumption of leverage is affirmed.
Kumar (2012) found that changes in the implied volatility index Ivix are negatively correlated to the returns of the Nifty 225 market index of the Indian stock market. Furthermore, he showed that during extreme stock market movements, this relationship becomes insignificant. Recently, Lee and Ryu (2013) underlined a negative and asymmetrical relationship between daily returns of the S & P 500 and KOSPI 200 and variations in VIX implied volatility index and VKOSPI respectively from both US and Korean markets. In addition, they found that for the Korean market negative shocks on returns play a dominant role while for US market, the positive impact of returns significantly influence the dynamic relationship returns-volatility index. Thus, these differences could be attributed to the specific characteristics and behaviour of the Korean options market. Fernandes et al. (2014) also showed that the relationship between daily changes in the VIX volatility index and contemporary performance of the market index S & P 500 is strongly negative during the period from 2 January 1992 to 15 January 2013. However, controlling asymmetric effects, they stated that there is no significant influence of the S & P 500 variations on the evolution of the VIX index for all time horizons considered in their study. Another recent study was conducted in the Korean market by Jung and Kim (2014) for the period from 2 January 2003 to 31 December 2011. They suggested that the assumptions of leverage and volatility feedback are unable to explain the asymmetrical relationship between the returns of the stock index KOSPI 200 and implied volatility VKOSPI. They concluded that this relationship could be driven by traders’ behaviour.
On the basis of this literature review, we propose to validate the following hypotheses:
H3: The implied volatility index variations are negatively related to contemporary returns of the underlying stock index.
H4: The implied volatility index varies asymmetrically to contemporary positive and negative returns variations of the underlying stock index.
H5: The underlying stock index variations have an impact on the implied volatility index "leverage hypothesis".
H6: The implied volatility index variation causes a variation on the underlying stock index "volatility feedback hypotheses."
3. DATA AND METHODOLOGY
The empirical study of our research focuses on two main themes: initially, we will study the relationship between implied volatility indices and the future volatility of the underlying stocks. Secondly, we will examine the relationship between implied volatility indices and returns of the underlying stocks.
As mentioned in the review of the above literature, studies on European markets remain poorly treated. Furthermore, we will particularly focus on 5 European market places namely the Euro zone, France, Germany, Switzerland and the United Kingdom for the period extending from January 1, 2010 to March 31 2015. We will use daily returns from closing prices for each series of implicit volatility indices and stock indices corresponding underlying throughout this selected period.
Our empirical study is based on two axes: firstly, we propose to evaluate the information content of each implied volatility index with respect to future market volatility as well as its predictive ability. To make this possible we propose a methodology inspired from Maghrebi et al. (2007).
On the other hand, concerning the relationship between implied volatility indices and the underlying stock returns, we will perform subsequently a Granger causality test to examine its direction.
3.1. Implied Volatility: Information Content
To validate the first set of hypotheses we will examine whether implied volatility indices contain information regarding future volatility of each relevant market. In the financial literature, crucial importance was given to GARCH models due to their ability to capture the volatility persistence and consolidation in the financial markets. We estimated the various GARCH specifications presented as follows:
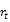 =
= 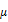 +
+ 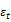 where
where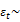 N (0,
N (0, 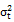 ) (1)
) (1)
Model-A: 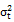 =
= 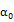 +
+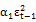 +
+ 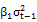 (2)
(2)
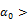 0 et
0 et 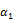 ,
, 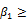 0 ;
0 ; 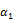 +
+ 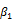 < 1
< 1
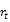 : the daily returns of the underlying stocks index
: the daily returns of the underlying stocks index
with: : 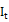 index of the underlying stocks at time t.
index of the underlying stocks at time t.
 : the average daily performance of the underlying stocks index.
: the average daily performance of the underlying stocks index.
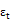 : error term capturing the innovation of daily output that is normally and independently distributed with zero mean and a conditional variance equal to
: error term capturing the innovation of daily output that is normally and independently distributed with zero mean and a conditional variance equal to 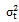 .
.
Model-B, GJR-GARCH (1,1) : 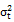 =
= 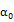 +
+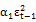 +
+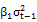 + λ
+ λ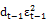 (3)
(3)
where: 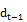 is an dumy variable
is an dumy variable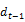 =
= 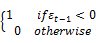
The GJR-GARCH model was introduced by Glosten et al. (1993) to consider the asymmetric response of market volatility to positive and negative shocks through the sign and significance of the parameter λ.
Thereafter, in order to assess the information content of each index of implied volatility, historical value and contemporary value of the latter are included as exogenous variables in equations (2) and (3) as shown by following formulas:
Model-C : 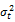 =
= 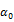 +
+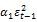 +
+ 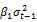 +
+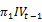 (4)
(4)
Model-D : 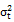 =
=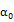 +
+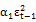 +
+ 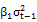 +
+ 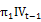 +
+ 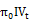 (5)
(5)
Model-E : 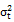 =
= 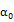 +
+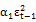 +
+ 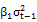 + λ
+ λ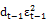 +
+ 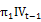 (6)
(6)
Model-F : 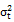 =
= 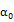 +
+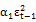 +
+ 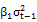 + λ
+ λ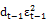 +
+ 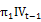 +
+ 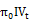 (7)
(7)
Where: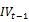 and
and 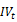 are respectively the past and current values of the implied volatility index at time t-1 and t. Hence, the parameters
are respectively the past and current values of the implied volatility index at time t-1 and t. Hence, the parameters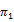 and
and 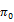 represent the information content of the implied volatility index in delayed and current values.
represent the information content of the implied volatility index in delayed and current values.
Estimation results of these GARCH models are presented in Tables 1, 2, 3, 4, and 5 below.
Table-1. Estimation results of GARCH for the index VSTOXX (Euro STOXX 50):
| Coefficient | Model-A | Model -B | Model -C | Model-D | Model -E | Model -F |
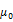 |
0.061*a | 0.075c | 0.031a | 0.001*** | -0.012***a | 0.103***a |
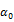 |
0.053***c | 0.051***c | -0.022***a | -0.030**c | -0.017***c | -0.012***b |
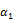 |
0.092*** | -0.029*** | -0.019 | 0.017*** | -0.056*** | -0.040*** |
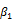 |
0.879*** | 0.892*** | -0.409** | 0.946*** | 0.792*** | 0.859*** |
| λ | - | 0.226*** | - | - | 0.303*** | 0.162*** |
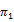 |
- | - | 0.019***b | -0.018***b | 0.016***c | -0.014***b |
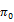 |
- | - | - | 0.019***b | - | 0.015***b |
| Log-V | 4016.053 | 4061.93 | 4053.322 | 4096.412 | 4076.029 | 4113.940 |
| Excess Log-V | - | 45.04 | 37.369 | 80.359 | 59.976 | 97.887 |
Notes: The A-F show the features of the conditional variance respectively defined by equations (2) to (7). *, ** And *** indicates that the coefficient is significant at the 10% level, 5% and 1% respectively. "Log-V" is the estimated function of Log-Likelihood and "Excess Log-V" means the Log-Likelihood excess relative to the model-A. For a clearer presentation, we multiplied the estimated values denoted by a, b and C respectively 102, 103 and 104.
Table-2. Estimation results of GARCH for the index VCAC (Euronext Paris)
| coefficient | Model-A | Model-B | Model-C | Model-D | Model-E | Model-F |
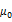 |
0.062**a | 0.014b | -0.034a | 0.142***a | -0.016a | 0.118***a |
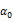 |
0.056***c | 0.059***c | -0.022***a | -0.046**c | -0.015***b | -0.019***c |
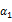 |
0.106*** | -0.026*** | -0.025 | 0.019*** | -0.049*** | -0.040*** |
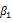 |
0.863*** | 0.869*** | -0.436*** | 0.940*** | 0.785*** | 0.832*** |
| λ | - | 0.255*** | - | - | 0.306*** | 0.167*** |
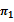 |
- | - | 0.021***b | -0.021***b | 0.016***c | -0.016***c |
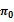 |
- | - | - | 0.021***b | - | 0.017***c |
| Log-V | 4042.075 | 4086.065 | 4079.769 | 4130.244 | 4100.238 | 4146.228 |
| Excess Log-V | - | 43.99 | 37.694 | 88.169 | 58.163 | 104.153 |
Notes: The A-F show the features of the conditional variance respectively defined by equations (2) to (7). *, ** And *** indicates that the coefficient is significant at the 10% level, 5% and 1% respectively. "Log-V" is the estimated function of Log-Likelihood and "Excess Log-V" means the Log-Likelihood excess relative to the model-A. For a clearer presentation, we multiplied the estimated values denoted by a, b and C respectively 102, 103 and 104.
Table-3. Estimation results of GARCH for the index VDAX-NEW (Frankfurt Stock Exchange)
| coefficient | Model-A | Model-B | Model-C | Model-D | Model-E | Model-F |
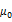 |
0.076***a | 0.057***a | 0.096***a | 0.173***a | 0.108**a | 0.164***a |
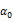 |
0.017***c | 0.026***c | -0.021***b | -0.015**c | -0.022***a | -0.068***c |
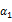 |
0.049*** | -0.007 | 0.011 | 0.009** | -0.010 | -0.031*** |
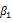 |
0.934*** | 0.930*** | -0.775*** | 0.961*** | -0.799*** | 0.913*** |
| λ | - | 0.096*** | - | - | 0.042*** | 0.072*** |
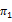 |
- | - | 0.019***b | -0.015***b | 0.019***b | -0.015***b |
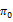 |
- | - | - | 0.016***b | - | 0.015***c |
| Log-V | 4323.310 | 4345.201 | 4398.266 | 4413.502 | 4400.816 | 4419.242 |
| Excess Log-V | - | 21.891 | 74.956 | 90.192 | 77.506 | 96.11 |
Notes: The A-F show the features of the conditional variance respectively defined by equations (2) to (7). *, ** And *** indicates that the coefficient is significant at the 10% level, 5% and 1% respectively. "Log-V" is the estimated function of Log-Likelihood and "Excess Log-V" means the Log-Likelihood excess relative to the model-A. For a clearer presentation, we multiplied the estimated values denoted by a, b and C respectively 102, 103 and 104.
Table-4.Estimation results of GARCH for the index VSMI (Swiss exchange)
| coefficient | Model-A | Model-B | Model-C | Model-D | Model-E | Model-F |
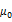 |
0.053**a | 0.031a | 0.018a | 0.129***a | 0.023a | 0.126***a |
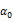 |
0.063***c | 0.072***c | -0.015***a | -0.039***c | -0.031***c | -0.078***c |
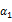 |
0.160*** | 0.062*** | 0.013 | 0.006 | -0.039** | -0.021*** |
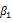 |
0.776*** | 0.754*** | -0.564*** | 0.929*** | 0.453*** | 0.851*** |
| λ | - | 0.222*** | - | - | 0.316*** | 0.073*** |
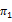 |
- | - | 0.017***b | -0.016***b | 0.044***c | -0.015***b |
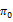 |
- | - | - | 0.017***b | - | 0.016***b |
| Log-V | 4500.593 | 4514.287 | 4533.085 | 4602.711 | 4544.214 | 4610.327 |
| Excess Log-V | - | 13.694 | 32.492 | 102.118 | 43.621 | 109.734 |
Notes: The A-F show the features of the conditional variance respectively defined by equations (2) to (7). *, ** And *** indicates that the coefficient is significant at the 10% level, 5% and 1% respectively. "Log-V" is the estimated function of Log-Likelihood and "Excess Log-V" means the Log-Likelihood excess relative to the model-A. For a clearer presentation, we multiplied the estimated values denoted by a, b and C respectively 102, 103 and 104.
Table-5. Estimation results of GARCH for the index VFTSE (London stock exchange)
| coefficient | Model-A | Model-B | Model-C | Model-D | Model-E | Model-F |
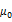 |
0.044**a | 0.069b | -0.010a | 0.106***a | 0.048b | -0.086***c |
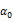 |
0.032***c | 0.034***c | -0.092***c | -0.026***c | -0.093***c | -0.073***c |
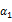 |
0.119*** | -0.022** | -0.019 | 0.109*** | -0.083*** | -0.095***c |
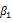 |
0.848*** | 0.872*** | -0.125 | 0.604*** | 0.777*** | 0.861*** |
| λ | - | 0.226*** | - | - | 0.306*** | 0.161*** |
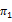 |
- | - | 0.011***b | -0.072***c | 0.013***c | -0.093***c |
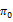 |
- | - | - | 0.010***b | - | 0.010***b |
| Log-V | 4473.338 | 4511.020 | 4504.928 | 4539.313 | 4532.752 | 4574.963 |
| Excess Log-V | - | 37.682 | 31.59 | 65.975 | 59.414 | 101.625 |
Notes: The A-F show the features of the conditional variance respectively defined by equations (2) to (7). *, ** And *** indicates that the coefficient is significant at the 10% level, 5% and 1% respectively. "Log-V" is the estimated function of Log-Likelihood and "Excess Log-V" means the Log-Likelihood excess relative to the model-A. For a clearer presentation, we multiplied the estimated values denoted by a, b and C respectively 102, 103 and 104.
Tables 1, 2, 3, 4 and 5 indicate that the various GARCH estimations results which confirm their validation for all sample indices. All coefficients of the conditional variance of returns 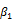 are less than unity. Thus, the parameter
are less than unity. Thus, the parameter 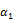 is positive and statistically significant for the whole sample. Hence, a shock on underlying stock index returns amplifies the volatility of the latter. While in model B, the impact of these returns shocks is asymmetric. For the entire sample, the parameter λ is positive: negative shocks affect more volatility than positive ones. Hence the presence of the phenomenon of leverage for the six studied European markets. We also notice that all the implied volatility indices contain relevant information about future the stock market’s volatility (the parameters
is positive and statistically significant for the whole sample. Hence, a shock on underlying stock index returns amplifies the volatility of the latter. While in model B, the impact of these returns shocks is asymmetric. For the entire sample, the parameter λ is positive: negative shocks affect more volatility than positive ones. Hence the presence of the phenomenon of leverage for the six studied European markets. We also notice that all the implied volatility indices contain relevant information about future the stock market’s volatility (the parameters 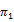 and
and 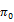 are all statistically significant). Therefore, the first hypothesis is confirmed.
are all statistically significant). Therefore, the first hypothesis is confirmed.
H1: The implied volatility index contains additional information compared to the volatility generated by the GARCH models.
Otherwise, 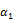 and
and 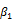 parameters are all significant for all markets of the sample. Market activity is concentrated over time. Periods of high volatility are more likely followed by periods of high volatility: volatility clustering effect documented by Mandelbrot (1963). While in considering the specification GARCH (1, 1) with the historical values of the implied volatility index VFTSE, we found a contradictory result to it. In this particular case, the VFTSE index remains the best measure of forecasting future volatility of the UK stock market. Hence, the second hypothesis H2 is invalidated except in this case. These estimation results from different GARCH specifications may be justified by the fact that options contracts for underlying stocks indices are inefficient as advanced by Martens and Zein (2004). The combination of GARCH and implied volatility indices respond to the needs of forecasting future volatility in European stock markets, see Day and Lewis (1992); Blair et al. (2001) and Becker et al. (2007).
parameters are all significant for all markets of the sample. Market activity is concentrated over time. Periods of high volatility are more likely followed by periods of high volatility: volatility clustering effect documented by Mandelbrot (1963). While in considering the specification GARCH (1, 1) with the historical values of the implied volatility index VFTSE, we found a contradictory result to it. In this particular case, the VFTSE index remains the best measure of forecasting future volatility of the UK stock market. Hence, the second hypothesis H2 is invalidated except in this case. These estimation results from different GARCH specifications may be justified by the fact that options contracts for underlying stocks indices are inefficient as advanced by Martens and Zein (2004). The combination of GARCH and implied volatility indices respond to the needs of forecasting future volatility in European stock markets, see Day and Lewis (1992); Blair et al. (2001) and Becker et al. (2007).
3.2. Implied Volatility Indices and the Underlying Stock Returns
In this section we will study the nature and the causality between implied volatility indices and contemporary performance of the stock underlying indices. To do this, we consider the following multiple linear regressions. We will realize later a Granger causality test:
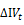 = α +
= α + 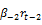 +
+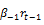 +
+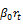 +
+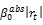
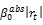 +
+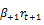 +
+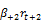 + 𝛾
+ 𝛾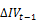 +
+ 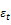 (8)
(8)
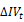 : daily variations of implied volatility index at time t.
: daily variations of implied volatility index at time t.
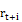 : daily returns from the market index of underlying stocks at time t+i
: daily returns from the market index of underlying stocks at time t+i  i = -2…2.
i = -2…2.
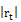 : daily returns in absolute value of the underlying stock index at time t.
: daily returns in absolute value of the underlying stock index at time t.
To validate the hypothesis stating that there is a negative relationship between contemporaneous returns of the underlying stocks index and implied volatility variations (H3), we expect a significant and negative value of the coefficient 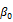 as evidenced by several studies as Fleming et al. (1995); Whaley (2000); Frijns et al. (2010); Ryu (2012) among others. In addition, considering the absolute value of contemporary daily returns from the underlying stock index allows us to highlight the existence of an asymmetrical relationship between implied volatility variations and current returns from underlying stocks indices. We expect as well that the
as evidenced by several studies as Fleming et al. (1995); Whaley (2000); Frijns et al. (2010); Ryu (2012) among others. In addition, considering the absolute value of contemporary daily returns from the underlying stock index allows us to highlight the existence of an asymmetrical relationship between implied volatility variations and current returns from underlying stocks indices. We expect as well that the 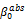 parameter to be of positive sign.
parameter to be of positive sign.
However, the sum of the coefficients β0 and 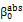 measures the asymmetry between changes of implied volatility and contemporary returns of the underlying stock indices.
measures the asymmetry between changes of implied volatility and contemporary returns of the underlying stock indices.
Table-6. Estimation results of the relationship between temporal changes in implied volatility indices and returns on equity indices underlying
| Coefficient | Euro zone | France | Germany | Switzerland | United Kingdom |
| α | -0.205***(-5.204) | -0.181***(-4.349) | 0.063(1.472) | -0.057**(-2.229) | -0.092***(-2.674) |
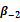 |
5.242***(2.598) | 4.390**(2.033) | 3.251(1.175) | 3.895**(2.013) | 0.234(0.095) |
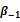 |
0.209(0.062) | -12.441***(-3.830) | 0.229(0.0685) | -7.022**(-2.343) | -5.766(-1.471) |
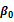 |
-100.559***(-50.064) | -90.724***(-42.374) | -70.109***(-23.667) | -83.465***(-43.006) | -112.140***(-45.962) |
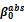 |
22.175***(7.586) | 20.325***(6.503) | -2.043(-0.515) | 11.542***(4.299) | 15.341***(4.315) |
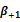 |
3.401*(1.695) | -1.149(-0.537) | -37.816***(-13.607) | -3.703*(-1.934) | 0.756(0.311) |
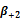 |
3.116(1.547) | 4.390(1.593) | 9.865***(3.584) | 5.082***(2.675) | -0.149(-0.061) |
| 𝛾 | -0.023(-5.204) | -0.120***(-4.349) | -0.097***(-3.507) | 0.025(0.919) | -0.024(-0.087) |
| R² adjusted | 0.661 | 0.584 | 0.392 | 0.619 | 0.617 |
Notes: This table presents the results of OLS estimates made on changes in implied volatility indices and stock market returns of underlying indices. α is the constant, β-2 is the coefficient of performance delayed to t-2 (lag = 2), β-1 is the coefficient of the delayed return to t-1 (lag = 1) β + 1 is the coefficient future return to t + 1 (lead = 1) β + 2 is the coefficient of future performance t + 2 (lead = 2), β0 is the coefficient of contemporary performance, β0abs is contemporary performance coefficient in absolute value and γ is the coefficient of the first difference of the delayed implied volatility index. *, ** And *** denote that the coefficient is significant at the 10%, 5% and 1%. Values shown in brackets are the values of the Student statistic (t-statistic).
Thus, if the stock market performance is positive then the coefficient affecting implied volatility index is equal to 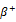 =
= 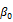 +
+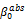 .
.
While if return is negative, implied volatility index is equal to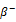 =
= 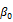 -
- 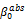 .
.
Furthermore, 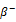 in absolute value is greater then
in absolute value is greater then 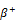 : negative returns of the underlying stock index have more impact on changes in the implied volatility index then positive ones.
: negative returns of the underlying stock index have more impact on changes in the implied volatility index then positive ones.
Estimation results of this regression are summarized in the table below.
In the context of the five studied European markets, 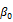 parameter is negative and statistically significant indicating that daily variations of implied volatility indices were negatively correlated with contemporaneous returns of the underlying stock indexes. Hence, the third hypothesis is affirmed for all equity markets. Similarly,
parameter is negative and statistically significant indicating that daily variations of implied volatility indices were negatively correlated with contemporaneous returns of the underlying stock indexes. Hence, the third hypothesis is affirmed for all equity markets. Similarly, 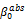 parameter is positive and statistically significant for European, French, English and Swiss markets. This entails that implied volatility indices vary asymmetrically to contemporary returns of underlying market indices. However, this result is contradictory to the one found on the German market (
parameter is positive and statistically significant for European, French, English and Swiss markets. This entails that implied volatility indices vary asymmetrically to contemporary returns of underlying market indices. However, this result is contradictory to the one found on the German market (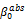 parameter is negative and statistically significant). This finding is in harmony with that found by the study of Dowling and Muthuswamy (2005) for the Australian market. Thus the hypothesis H4 is valid unless for the German market.
parameter is negative and statistically significant). This finding is in harmony with that found by the study of Dowling and Muthuswamy (2005) for the Australian market. Thus the hypothesis H4 is valid unless for the German market.
H4: The implied volatility index varies asymmetrically to contemporary positive and negative returns variations of the underlying stock index.
H5: The underlying stock index variations have an impact on the implied volatility index "leverage hypothesis".
H6: The implied volatility index variation causes a variation on the underlying stock index "volatility feedback hypotheses."
Finally, Granger causality test revealed several findings that differ from one market to another. For euro zone and Germany, implied volatility index variations Granger causes contemporary returns of underlying stock indexes. Therefore, the sixth assumption is confirmed. For the French market, we found a contradictory result which leads us to confirm the existence leverage effect (H5). Otherwise, for the Swiss stock market, we found bidirectional causality between volatility index VSMI variations and contemporary performance of the market index SMI. Hypotheses H5 and H6 are valid in this case. However, for the UK market, no causal link was found significant this can be explained by the fact that there are other factors (behavioural factors) that could explain the origin of this relationship as advanced by Jung and Kim (2014).
4. CONCLUSION
The development of various implied volatility indices on the international stock markets has attracted the attention of several researches. A variety of empirical studies have attempted to explore the relationship between implied volatility indices and stock market returns variations (spot market). It turned out interesting to dedicate this research to the study of the nature of the relationship between the implied volatility indices and returns from the underlying stocks indices from different European countries namely the Euro zone, France, Germany, Switzerland and the United Kingdom.
We investigated the nature of the relationship between implied volatility indices observed on five financial centers and contemporary performance of the underlying stocks indices and their predictive power with regard to the future volatility of the corresponding stock market.
Our results show that all the implied volatility indices contain relevant information concerning both the returns and future volatility of the underlying stock market. For stock market returns, we found that there is a negative and asymmetrical relationship between implied volatility indices. While this asymmetrical relationship was not verified on the German market. Concerning future volatility forecasting, we found that all the implied volatility indices contain relevant information.
Furthermore, implied volatility indices considered in our study provide important information on the European underlying stock markets which is interesting for various categories of investors.
Thus, this paper contributes to the existing empirical literature in different ways. First, studies of the relationship between implied volatility indices and stock indices are concentrated particularly on the US stock markets and more recently Asian ones (Korea, India, Japan, etc.). We propose to fill in this gap by focusing on European markets. On the other hand, our study uses a sample of several implied volatility indices while almost all previous researches focus only on one implied volatility index or on a smaller sample.
For future research it would be interesting to study the phenomenon of transmission of volatility between several international stock markets and the impact of macroeconomic announcements and the rating of sovereign debt on the evolution of implied volatility indices.
| Funding: This study received no specific financial support. |
| Competing Interests: The authors declare that they have no competing interests. |
| Contributors/Acknowledgement: All authors contributed equally to the conception and design of the study. |
REFRENCES
Aboura, S., 2005. Le comportement des indices de volatilité implicite internationaux. Revue Bancaire et Financière, 7(8): 457-460.
Baker, M. and J. Wurgler, 2006. Investor sentiment and the cross-section of stock returns. Journal of Finance, 61(4): 1645–1680.
Banerjee, A. and R. Kumar, 2011. Realized volatility and India VIX, Working Paper, Indian Institute of Management Calcutta, No. 688.
Becker, R., A.E. Clements and S.I. White, 2007. Does implied volatility provide any information beyond that captured in model-based volatility forecasts. Journal of Banking & Finance, 31(2007): 2535-2549.
Black, F. and M. Scholes, 1973. The pricing of options and corporate liabilities. Journal of Political Economy, 81(3): 637-654.
Blair, B.J., S.H. Poon and S.J. Taylor, 2001. Forecasting s&p 100 volatility: The incremental information content of implied volatilities and high frequency index returns. Journal of Econometrics, 105: 5–26.
Corrado, C.J. and J.T.W. Miller, 2005. The forecast quality of CBOE implied volatility indexes. Journal of Futures Markets, 25(4): 339-373.
Day, T.E. and C.M. Lewis, 1992. Stock market volatility and the information content of stock index options. Journal of Econometrics, 52(1-2): 267-287.
Dowling, S. and J. Muthuswamy, 2005. The implied volatility of australian index options. Working Paper, SSRN, 500165.
Fernandes, M., M.C. Medeiros and M. Scharth, 2014. Modeling and predicting the CBOE market volatility index. Journal of Banking & Finance, 40(2014): 1–10.
Fleming, J., B. Ostdiek and R.E. Whaley, 1995. Predicting stock market volatility: A new measure. Journal of Futures Markets, 15(3): 265-302.
Frijns, B., C. Tallau and A. Tourani-Rad, 2010. The information content of implied volatility: Evidence from Australia. Journal of Futures Markets, 30(2): 134–155.
Giot, P., 2005. Relationships between implied volatility indexes and stock index returns. Journal of Portfolio Management, 31(3): 92–100.
Glosten, L., R. Jaganathan and D. Runkle, 1993. On the relation between the expected value and the volatility of the nominal excess return on the stocks. Journal of Finance, 48(4): 1779–1801.
Hibbert, A.M., R.T. Daiglerb and B. Dupoyet, 2008. A behavioral explanation for the negative asymmetric return–volatility relation. Journal of Banking & Finance, 32(2008): 2254–2266.
Hull, J., 2011. Options futures et autres actifs dérivés. 8th Edn.: Edition Pearson.
Jung, D. and T. Kim, 2014. An analysis of the effects of index returns on the asymmetry of implied volatility. Advanced Science and Technology Letters, 57(Business 2014): 31-34.
Koopman, S.J., B. Jungbacker and E. Hol, 2005. Forecasting daily variability of the S&P 100 stock index using historical, realized and implied volatility measurements. Journal of Empirical Finance, 12: 445-475.
Kumar, S.S.S., 2012. Afirst look at the properties of India’s volatility index. International Journal of Emerging Markets, 7(2): 160-176.
Lee, B.S. and D. Ryu, 2013. Stock returns and implied volatility: A new VAR approach. Economics-Ejournal.Ja, 3(7): 1-20.
Maghrebi, N., M.-S. Kim and K. Nishina, 2007. The KOSPI200 implied volatility index: Evidence of regime switches in volatility expectations. Asia-Pacific Journal of Financial Studies, 36(2): 163-187.
Martens, M. and J. Zein, 2004. Predicting financial volatility: High frequency time-series forecasts vis-à-vis implied volatility. Journal of Futures Markets, 24(11): 1005–1028.
Masset, P. and M. Wallmeier, 2010. A high-frequency investigation of the interaction between volatility and DAX returns. European Financial Management, 16(3): 327–344.
Padhi, P. and I. Shaikh, 2014. On the relationship of implied, realized and historical volatility: Evidence from NSE equity index options. Journal of Business Economics and Management, 15(5): 915–934.
Ryu, D., 2012. Implied volatility index of KOSPI200: Information contents and properties. Emerging Markets Finance & Trade, 48(2): 24–39.
Simon, D.P., 2003. The nasdaq volatility index during and after the bubble. Journal of Derivatives, 11(2): 9-24.
Siriopoulos, C. and A. Fassas, 2008. The information content of VFTSE. Working Paper, SSRN, No. 1307702.
Thenmozhi, M. and A. Chandra, 2015. On asymmetric relationship of India volatility index (India VIX) with stock market return and risk management. Working Paper, Indian Institute of Management Calcutta, Springer.
Whaley, R.E., 1993. Derivatives on market volatility: Hedging tools long overdue. Journal of Derivatives, 1(1): 71-84.
Whaley, R.E., 2000. The investor fear gauge. Journal of Portfolio Management, 26(3): 12–17.
| Views and opinions expressed in this article are the views and opinions of the author(s), Asian Economic and Financial Review shall not be responsible or answerable for any loss, damage or liability etc. caused in relation to/arising out of the use of the content. |






